Messfehler/Messungenauigkeit Temperaturmessung 2-Leiter, 3-Leiter vs. 4 Leiter PT100

Wer sich im industriellen Bereich mit Prozesstechnik und deren Automatisierung befasst, hat es auch immer wieder mit Temperaturmessungen zu tun. In den unteren Temperaturbereichen bis 300°C-400°C werden dann in den meisten Fällen PT100-Widerstandsthermometer eingesetzt. Der PT100-Widerstand kann aber in verschiedenen Schaltungsvarianten an den Messumformer angeschlossen werden. Dabei dienen die 3-Leiterschaltung und 4-Leiter-Schaltung der Kompensation des Leitungswiderstandes, während die 2-Leiter-Schaltung eine solche Kompensation nicht aufweist.

Das eine solche Kompensation gut ist, liegt auf der Hand, aber es stellt sich dann die Frage, ob man die 3- oder 4-Leiter-Schaltung einsetzen sollte. Ebenfalls allgemein bekannt ist, dass die Vier-Leiterschaltung eine bessere Widerstandskompensation ermöglichts. Aber wie groß ist wirklich der Genauigkeitsunterschied zwischen 3-Leiter und 4-Leiter PT100 und dass ggf. auch noch in Abhängigkeit von Leitungslänge oder Leitungslängendifferenzen? Und haben diese Unterschiede überhaupt eine praktische Relevanz oder bewegen sich die Unterschiede im akademischen Genauigkeitsbereich und sind eher was für Präzisions-, Labor- oder Kalibriermessgeräte?

In Kürze

Diejenigen, die die schnelle Antwort suchen, springen oder scrollen zur untenstehenden Tabelle mit den exemplarisch berechneten Messfehlern einer Zweileiterschaltung. Die Zwei-Leiter-Schaltung führt zu den größten Messfehlern in Abhängigkeit der Länge der Leiter, z.B. ca. 0,4 K bei 1m oder ca. 20 K bei 50m.

Die Drei-Leiter-Schaltung kompensiert den Leitungswiderstand vollständig unter der Annahme, dass die Anschlussleitungen gleich lang sind, aus demselben Material bestehen und denselben Querschnitt haben. Diese Annahme ist in der Praxis und den meisten industriellen Anwendungen zutreffend und Montage- und Fertigungsabweichungen so gering, dass diese in Bezug auf den sich daraus ergebenen Messfehler nicht ins Gewicht fallen. Somit gibt es keinen validen Grund, insbesondere bei kurzen Anschlussleitungen, wie in Kopftransmittern, den 3-Leiter-Anschluss nicht zu verwenden.

Die Vier-Leiterschaltung kompensiert den Leitungswiderstand vollständig, auch wenn die Leitungslängen der Anschlussleitungen in Länge, Querschnitt, Material differieren. Damit eignet sie sich für sehr präzise Messungen, um Fertigungstoleranzen bei den Anschlussleitungen auszumerzen, oder für Sonderfälle in der Montage, wo tatsächlich bei den Anschlussleitungen Differenzen in der Länge auftreten.

Wie funktionieren PT100-Temperaturmessungen als Zwei-Leiter-, Drei-Leiter- und Vier-Leiter-Schaltung?

Bekanntermaßen ist ein elektrischer Widerstand temperaturabhängig. Dies macht man sich bei der Temperaturmessung zu nutzen, in dem man einen Platin-Widerstand von 100 Ohm (Pt100) oder von 1000 Ohm (PT1000) verwendet. Die genannten Ohm-Zahlen gelten als Nennwiderstand für 0°C. Ein Messumformer, Transmitter oder Auswertegerät, wie man es auch immer nennen möchte, prägt einen definierten Strom ein (Stromquelle). Über den nun messbaren Spannungsfall lässt sich der aktuelle temperaturabhängige Widerstand bestimmen.

$R = \frac{U}{I}$

Zwei-Leiter-Schaltung

Die Verbindung des PT100 erfolgt hier ausschließlich über zwei Drähte mit dem Messumformer. Es wird klar, wenn man sich das Bild anschaut, dass die Leitungen selbst in diesem Fall auch einen Leitungswiderstand einbringen, dessen Größe unter anderem abhängig ist von der Leitungslänge. Es wird also nicht der exakte Widerstand vom PT100-Element gemessen, was zu einem Messfehler führt.

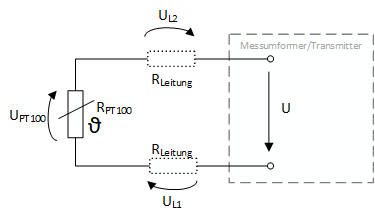
Schaltbild einer 2-Leiter-Schaltung bei PT100 Widerstandstemperaturmessung — PT100 Zwei-Leiter-Schaltung

Drei-Leiter-Schaltung

Bei der 3-Leiter-Schaltung sind 3 Leiter an den PT100-Widerstand angeschlossen. Über zwei Leitungen davon, gekennzeichnet mit den Widerständen $R_{L1}$ und $R_{L2}$ wird der Messstrom $I_{M}$ eingeprägt. Dieser erzeugt ebenfalls einen Spannungsfall. Über den dritten Leiter mit dem Leitungswiderstand $R_{L3}$ erfolgt die hochohmige Spannungsmessung. Dadurch fließt kein bzw. nahezu kein Strom über den dritten Leiter und somit entsteht auch kein Spannungsfall über den Dritten Leiter, der sich als Messfehler auswirkt. Es bleibt aber der Spannungsfall über den Leitungswiderstand $R_{L1}$ , der sich theoretisch als Messfehler auswirkt. Wie und unter welcher Annahme der Messfehler eliminiert werden kann, zeigt die folgenden mathematische Herleitung. Wie man in der mathematischen Herleitung sehen wird, erfolgt hier nur die Kompensation des Leitungswiderstands, wenn beide Leiter (Hin- und Rückleiter) gleich lang sind. Davon kann aber in den meisten praktischen Anwendungsfällen ausgegangen werden, da alle drei Adern beim Messumformer/Auswertgerät angekommen müssen und nicht als Einzeldrähte über verschiedene Wege verlegt werden.

Wie sich bei der der Drei-Leiterschaltung der Messfehler/Spannungsfall über den Leitungswiderstand herausrechnen lässt

Als erstes stellen wir die beiden Maschengleichungen auf:

$U_{1} = I_{m} (R_{L 1} + R_{L 2} + R_{P T 100})$

$U_{2} = I_{m} (R_{L 1} + R_{P T 100})$

Dann berechnen wir die Spannungsdifferenz:

$∆ U = U_{1} - U_{2}$

$∆ U = I_{m} R_{L 2}$

Darüber lässt sich dann der Spannungsfall über den Leiter $R_{L 2}$ berechnen

$\frac{∆ U}{I_{m}} = R_{L 2}$

Nun kommt unsere Voraussetzung zum tragen, dass sowohl Hin- als auch Rückleiter gleich lang sind:

$R_{L 2} = R_{L 1}$

Somit können wir $R_{L 1}$ mit $\frac{∆ U}{I_{m}}$ ersetzen in der Gleichung für $U_{2}$ , dem Spannungsmesskreis:

$U_{2} = I_{m} (\frac{∆ U}{I_{m}} + R_{P T 100})$

Damit haben wir alle bekannten und messbaren Größen, um den realen Widerstand des Pt100 ohne Leitungswiderstand z.B. im Mikroprozessor des Messumformers zu berechnen, indem man die Gleichung noch wie folgt umstellt:

$R_{P T 100} = \frac{U_{2} - ∆ U}{I_{m}} = \frac{2 U_{2} - U_{1}}{I_{m}}$

Vier-Leiter-Schaltung

Wie man im nachfolgenden Bild sieht, sind bei der 4-Leiter-Schaltung vier Drähte an dem Temperaturwiderstand angeschlossen. In diesem Fall wird der Messstrom über die beiden Leitungen mit den Leitungswiderständen $R_{L1}$ und $R_{L2}$ eingeprägt. Über die anderen beiden Leitungen, $R_{L3}$ und $R_{L4}$ erfolgt ausschließlich die hochohmige Spannungsmessung. Dadurch fließt kein bzw. nahezu kein Strom über $R_{L3}$ und $R_{L4}$ und erzeugt somit auch keinen Spannungsfall. Der Spannungsfall entsteht ausschließlich über $R_{L1}$ , $R_{L2}$ und $R_{PT100}$ .

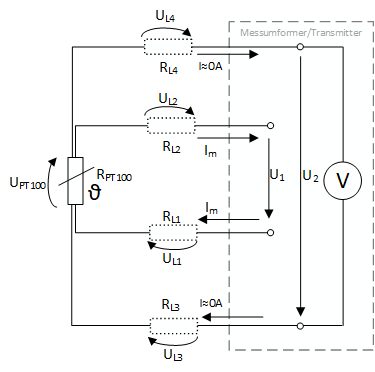
Wie sich bei der der 4-Leiterschaltung der Messfehler/Spannungsfall über den Leitungswiderstand herausrechnen lässt

Wie sähe also die Berechnungsformel für den realen Pt100-Widerstand in einem Mikroprozessor des Auswertegerätes aus? Wieder stellen wir die Maschengleichungen auf:

$U_{1} = I_{m} (R_{L 1} + R_{L 2} + R_{P T 100})$

$U_{2} = I_{m} R_{P T 100}$

In diesem Fall ist der reale Pt100-Widerstand ganz einfach die gemessene Spannung $U_{2}$ dividiert durch den Messstrom $I_{m}$ :

$R_{P T 100} = \frac{U_{2}}{I_{m}}$

Über die Bildung des $∆ U$ sehen wir, dass die Summe der Leitungswiderstände übrig bleibt:

$∆ U = U_{1} - U_{2}$

$∆ U = I_{m} (R_{L 1} + R_{L 2})$

$\frac{∆ U}{I_{m}} = R_{L 1} + R_{L 2}$

Theoretische Berechnung der Messungenauigkeit

Formel für Widerstand-Temperaturabhängigkeit

Um den Messfehler zu bestimmen verwenden wir hier die Callendar-Van-Dusen-Gleichung (Quelle Wikipedia), welche den Zusammenhang zwischen Widerstand und Temperatur beschreibt von Platin-Widerstandsthermometern.

$R (T) = R_{0} (1 + A T + B T^{2}) w e n n 0 ° C \leq T \leq 661 ° C$

$R (T) = R_{0} [1 + A T + B T^{2} + C (T - 100) T^{3}] w e n n - 200 ° C < T < 0 ° C$

Die Parameter A, B, C sind experimentell bestimmte Konstanten. Und $R_{0}$ ist der Widerstandswert bei 0°C; also 100 Ohm beim PT100. Für die Parameter A, B, C werden folgende Werte verwendet (Quelle: Richtlinie DKD-R 5-6 Physikalisch Technische Bundesanstalt)

$A = 3, 9107762809 E - 03 \frac{1}{° C}$

$B = - 5, 7693522900 E - 07 \frac{1}{° C^{2}}$

$C = - 1, 1855984344 E - 11 \frac{1}{° C^{4}}$

Löst man die quadratische Gleichung nach T, dann sieht es wie folgt aus:

$T_{1 / 2} = - \frac{A}{2 B} \pm \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R (T)}{B R_{0}}}$

wobei nur die folgende Lösung sinnvolle praxisrelevante Ergebnisse liefert:

$T = - \frac{A}{2 B} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R (T)}{B R_{0}}}$

Herleitung Messfehler bei der 2-Leiterschaltung

Nun kann man noch R(T) ersetzen mit dem gemessenen Widerstand, der sich aus dem Platin-Widerstand und dem Leistungswiderstand zusammensetzt, wobei hier angenommen ist, das Hin- und Rückleitung gleich lang sind und denselben Querschnitt haben

$R (T) = R_{m} = R_{P T 100} + R_{L 1} + R_{L 2} = R_{P T 100} + \frac{2 ρ l}{A_{C u}}$

Nun kann man einmal die Temperatur nur des PT100 berechnen und einmal die Temperatur, die sich inklusive Leitungswiderstand ergibt.

$T_{2 L e i t e r} = - \frac{A}{2 B} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} + \frac{2 ρ l}{A_{C u}}}{B R_{0}}}$

$∆ T = T_{2 L e i t e r} - T_{P T 100} = \frac{A}{2 B} + \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} (T)}{B R_{0}}} - \frac{A}{2 B} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} (T) + \frac{2 ρ l}{A_{C u}}}{B R_{0}}}$

$∆ T = T_{2 L e i t e r} - T_{P T 100} = \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} (T)}{B R_{0}}} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} (T) + \frac{2 ρ l}{A_{C u}}}{B R_{0}}}$

Mathematisch gewiefte Kerle können die Subtraktion der beiden Wurzelausdrücke bestimmt noch vereinfachen. Für die Berechnung des Messfehlers mittels Excel soll das aber genügen. Es bleibt dabei zu beachten, dass wir hier davon ausgehen das beide Leiter gleich lang sind. Außerdem nimmt die Formel an, dass der Leitungswiderstand konstant ist. Es wird also nicht berücksichtigt, dass in der Praxis der Leitungswiderstand ebenfalls temperaturabhängig ist und über die Wärmeleitung ein entsprechendes Temperaturprofil vom Sensor bis zum Messumformer sich aufbauen wird. Für die praktische Näherung sollte dies aber nicht ins Gewicht fallen.

Berechnung des Messfehlers für die Zwei-Leiterschaltung

Da nun das Formelwerk steht, können wir den theoretischen Messfehler berechnen. Wir nehmen eine Pt-100-Anschlussleitung, wie man sie auch kaufen kann aus Kupfer. Dafür setzen wir die folgenden Konstanten an:

Spezifischer Widerstand Kuper: $ρ_{C u} = 0, 01786 \frac{Ω m m^{2}}{m}$

Querschnitt Leitung: $A_{C u} = 0, 22 m m^{2}$

Die nachfolgende Tabelle zeigt die Messfehler in Kelvin (K), die sich aufgrund des Leitungswiderstands ergeben für verschiedene Leitungslängen und für verschiedene Temperaturen bzw. Widerstandswerte am PT100.

Widerstand/Länge	Temperatur	1 m	10 m	20 m	30 m	40 m	50 m
100 Ohm	0 °C	0,415 K	4,154 K	8,314 K	12,478 K	16,648 K	20,822 K
125 Ohm	64,54 °C	0,423 K	4,235 K	8,475 K	12,721 K	16,972 K	21,229 K
150 Ohm	130,36 °C	0,432 K	4,321 K	8,647 K	12,979 K	17,317 K	21,661 K
175 Ohm	197,53 °C	0,441 K	4,412 K	8,830 K	13,253 K	17,684 K	22,120 K
200 Ohm	266,15 °C	0,451 K	4,509 K	9,024 K	13,546 K	18,074 K	22,609 K

Man erkennt relativ deutlich, dass die Abhängigkeit des Messfehlers von der Temperatur sich nur geringfügig bemerkbar macht, wohl bemerkt, dass die Temperaturabhängigkeit des Leitungswiderstands hier nicht mit eingeht.
Deutlich hingegen zeigt sich aber die Abhängigkeit von der Länge. Bei 50m würde sich bei den angenommenen Werten ein Messfehler von ca. 20 Kelvin einstellen.
Geht man jedoch von einen Kopftransmitter aus, wo die Leitungslänge zwischen 20cm - 50cm betragen dürfte, bewegen sich die Messungenauigkeiten zwischen 0,09K und 0,2K, was für viele praktische Anwendungsfälle auch genügen könnte.

Messungenauigkeit zwischen 2- Leiter und 4-Leiter Pt100

Wie wir oben gesehen haben, kompensiert die Vierleiterschalung sämtliche Leitungswiderstände auch wenn diese einen unterschiedlichen Querschnitt, ein unterschiedliche Material oder unterschiedliche Längen haben. Somit stellt sich die Formel, die wir oben für die Zweileiterschaltung schon mal definiert haben, wie folgt dar:

$R (T) = R_{m} + R_{L 1} + R_{L 2} = R_{P T 100} + \frac{ρ_{1} l_{1}}{A_{C u 1}} + \frac{ρ_{2} l_{2}}{A_{C u 2}}$

Nun kann man das wieder für R(T) einsetzen und man erhält noch schönere Terme:

$T_{L e i t e r} = - \frac{A}{2 B} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} + \frac{ρ_{1} l_{1}}{A_{C u 1}} + \frac{ρ_{2} l_{2}}{A_{C u 2}}}{B R_{0}}}$

$∆ T = T_{L e i t e r} - T_{P 100} = \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100}}{B R_{0}}} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} + \frac{ρ_{1} l_{1}}{A_{C u 1}} + \frac{ρ_{2} l_{2}}{A_{C u 2}}}{B R_{0}}}$

Um einen potentiellen Messfehler zu berechnen, kann man diese Formel benutzen, exemplarisch oder beispielhaft darstellen lässt sich das nicht mehr in einer Tabelle. Hierfür bedarf es dann ein mehrdimensionales Array. Dem Grunde nach werden sich die Abweichungen aber um die in der oben dargestellten Tabelle bewegen bzw. entsprechend der Längendifferenz unterhalb des Wertes in der Tabelle liegen für die jeweilig größte Länge.

Welchen Messfehler gibt es zwischen 3-Leiter und 4-Leiter Pt100?

Hier kratzt sich der Praktiker langsam am Kopf, ob solche Betrachtungen noch Sinn machen; denn hier muss man unterstellen, dass die beiden Anschlussleitungen (Hin- und Rückleiter) nicht dieselbe Länge und/oder nicht denselben Querschnitt haben oder sogar aus anderen Materialien bestehen. Aber es mag Anwendungsfälle in der Labor- und Kalibriertechnik geben, wo das eine Rolle spielt.
Welcher Fehler kann nun entstehen zwischen der Dreileiterschaltung und Vierleiterschaltung? Dazu müssen wir erstmal konstatieren, dass die Leitungswiderstände $R_{L 1}$ und $R_{L 2}$ nicht gleich sind und aufgrund unterschiedlicher Längen, Materialien oder Querschnitte zu einem Messfehler führen. Um es nicht allzu kompliziert zu machen, nehmen wir mal an, dass es nur um unterschiedliche Längen geht.

$R_{L 1} \neq R_{L 2}$

$\frac{ρ l_{1}}{A_{C u}} \neq \frac{ρ l_{2}}{A_{C u}}$

Der Unterschied bildet sich in einer Differenz der Widerstände ab, die sowohl negativ als auch positiv sein kann.

$∆ R = \frac{ρ (l_{1} - l_{2})}{A_{C u}}$

$∆ R = \frac{ρ ∆ l}{A_{C u}}$

$R_{L 2} = R_{L 1} + ∆ R$

Der Temperaturunterschied zwischen real und gemessen würde sich also entsprechend der oben bestimmten Formeln wie folgt berechnen lassen:

$∆ T = T_{L e i t e r} - T_{P T 100} = \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100}}{B R_{0}}} - \sqrt{\frac{A^{2} - 4 B}{4 B^{2}} + \frac{R_{P T 100} + \frac{ρ ∆ l}{A_{C u}}}{B R_{0}}}$

Damit ergeben sich quantitativ dieselben Werte, wie in der Tabelle oben dargestellt nur mit der Interpretation, dass es sich in diesem Fall nicht um die Leitungslänge, sondern um die Leitungslängendifferenz handelt. Bei 1 m Leitungsdifferenz hat man also einen Messfehler von ca. 0,4 K und bei 10 m von ungefähr 4 K. Aber mal ehrlich, wenn man in der Praxis, solche Leitungsdifferenzen hat, hat etwas in der Montage verkehrt gemacht.

In der Präzisionsmesstechnik mag aber der Ausschluss von solchen Differenzen aber durchaus berechtigt sein. Schließlich können durch Fertigungstoleranzen Unterschiede im Querschnitt auftreten oder im Leitwert. Außerdem ist der Leitwert auch nicht über die gesamte Länge konstant aufgrund des Temperaturprofils das sich vom Sensor (Pt100) bis zum Messumformer ausbildet.

[Datum: 13.09.2025]