Spannungsfall auf elektrischen Leitungen

Über alle elektrischen Leitungen, über denen ein Strom von einem Erzeuger bzw. einer Spannungs- oder Stromquelle zu einem Verbraucher fließt, entsteht aufgrund des eigenen Widerstands der Leitung ein Spannungsfall $Δ U$ . Damit am Verbraucher noch die erforderliche Nennspannung $U_{N}$ ankommt, müssen die Zuleitungen entsprechend dimensioniert werden. Die entscheidenden Einflussgrößen sind dabei der elektrische Widerstand der Leitung:

Formel 1: $R_{L} = \frac{2 L}{κ A}$

$L [m]$ ...Länge der Leitung

$A [m m^{2}]$ ...Querschnitt der Leitung

$κ [\frac{m}{Ω m m^{2}}]$ ...materialabhängige Leitfähigkeit

sowie die Nenndaten der angeschlossenen Verbraucher:

$U_{N} [V]$ ...Nennspannung des Verbrauchers

$P_{N} [W]$ ...Nennleistung des Verbrauchers

Da der zulässige Spannungsfall $Δ u_{z u l}$ in den einschlägigen Normen und Richtlinien meistens in Prozent angegeben wird, berechnet man den prozentualen Spannungsfall $Δ u$ :

Formel 2: $Δ u = \frac{Δ U}{U_{N}}$

$Δ u \leq Δ u_{z u l}$

Spanungsfall Allgemein

Im Internet und mit Bezug auf die Norm DIN VDE 0100-520 Anhang G wird für den Spannungsfall die allgemeine Formel angegeben:

Formel 3: $Δ U = b I_{b} (\frac{L}{κ A} \cos (ρ) + λ L \sin (ρ))$

$I_{B}$ ...Betriebsstrom

$b$ ...Koeffizient der Anzahl der zu berücksichtigenden Zuleitungen

$λ$ ...Blindwiderstand je Längeneinheit des Leiters

$\cos (ρ)$ ...Leistungsfaktor des bzw. der Verbraucher

Bei den nachfolgenden Formeln für Gleich-, Wechsel- und Drehstrom wird der induktive Widerstand der Leistung X=0 angenommen.

$Δ U = \frac{b L}{κ A} I_{b} c o s (ρ)$

Aber auch so sorgt die Formel noch für etwas Verwunderung. Denn

$I_{W} = I_{b} c o s (ρ)$

betrachtet nur den Wirkanteil des Stromes. Bekanntermaßen fließt aber über die Zuleitungen auch der Blindanteil des Stroms und trägt somit seinen Anteil zur Erwärmung der Leitungen bei. In diesen Formeln stecken also viele Vereinfachungen:

es wird eine konstante Temperatur für die Zuleitung angenommen. Bekanntlich erwärmt sich die stromführende Zuleitung und der Widerstand nimmt mit steigender Temperatur zu
es wird der induktive Widerstand der Zuleitungen vernachlässigt
es wird der kapazitive Widerstand der Zuleitungen vernachlässigt
es wird nur der Wirkanteil berücksichtigt
es wird der $c o s (ρ)$ des Verbrauchers als konst. angenommen. Würde man induktive und kapazitive Widerstände in den Scheinwiderstand mit einrechnen, würde sich auch ein leicht abweichender $c o s (ρ)$ einstellen
stattdessen addiert die Formel 3 den Wirkanteil der Spannung mit dem Blindanteil, wo man sonst den Betrag nehmen würde.

Man muss sich also bewusst sein, dass es sich hierbei nur um Näherungsformeln handelt.

Spannungsfall für Gleichstrom

Beim Gleichstrom wirkt im stationären Zustand nur die ohmsche Last $\cos (ρ) = 1$ . Damit ergibt sich der Spannungsfall in Abhängigkeit vom Betriebsstrom $I_{B}$ :

Formel 4: $Δ U = R \cdot I_{B} Δ U = \frac{2 L I_{B}}{κ A}$

Verwendet man die Nennleistung und -spannung der angeschlossenen Verbraucher ergibt sich folgende Formel:

Formel 5: $Δ U = \frac{2 L P_{N}}{κ A U_{N}}$

Spannungsfall für einphasigen Wechselstrom

Bei einphasiger Wechselspannung berechnet sich der Spannungsfall über die Leitung in Abhängigkeit vom Betriebsstrom wie folgt:

Formel 6: $Δ U = \frac{2 L I_{B} \cos (ρ)}{κ A}$

Anhand der Formel sieht man, dass eigentlich nur der Wirkanteil des Stroms berücksichtigt wird. Dies zeigt auch die folgende Formel, welche den Spannungsfall in Abhängigkeit von der Wirkleistung berechnent.

Formel 7: $Δ U = \frac{2 L P_{N}}{κ A U_{N}}$

Spannungsfall für dreiphasigen Wechselstrom (Drehstrom)

Bei dreiphasiger Wechselspannung (Drehstrom) berechnet sich der Spannungsfall über die Leitung in Abhängigkeit vom Betriebsstrom wie folgt:

Formel 8: $Δ U = \frac{\sqrt{3} L I_{B} \cos (ρ)}{κ A}$

Auch hier sieht man anhand des Verkettungsfaktors und des Leistungsfaktors, dass nur der Wirkanteil eingeht. Über eine gegebene Leistung berechnet sich der Spannungsfall wie folgt:

Formel 9: $Δ U = \frac{L P_{N}}{κ A U_{N}}$

Theoretische Erläuterungen

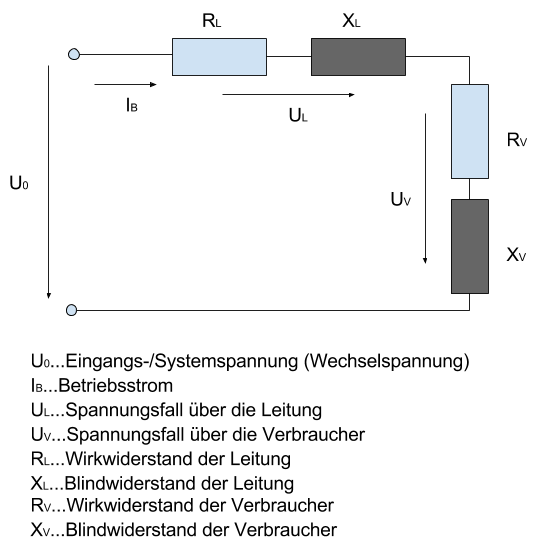
Wie bereits erwähnt, handelt es sich bei den oben genannten Formeln um Näherungsformeln, die nur unter den passenden Randbedingungen eingesetzt werden sollten. Will man es genauer machen; ich sage explizit nicht exakt; sollte man sich den Sachverhalt erst einmal in einem Ersatzschaltbild verdeutlichen. Das nachfolgende Bild zeigt die Leitungswiderstände (ohmscher Widerstand und Blindwiderstand) in Reihenschaltung zum Widerstand der Verbraucher, welche sich ebenfalls aus Wirk- und Blindwiderstand zusammensetzen. Der Blindwiderstand kann sich jeweils unterschiedlich aus kapazitiven und induktiven Blindwiderstand zusammensetzen. Auch die Zuleitungen können solche Anteile aufweisen. Es wird hier von einphasigen Wechselstrom ausgegangen.

Bild: Ersatzschaltbild Reihenschaltung Leitungs- und Verbraucherwiderstand

Im Zeigerdiagramm sieht man wie sich aus der Reihenschaltung prinzipiell der resultierende Scheinwiderstand zusammensetzt.

Bild: Zeigerdiagramm

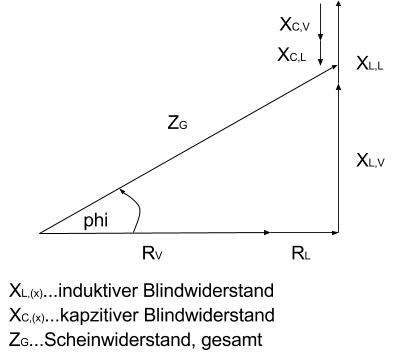
Auch lässt sich im Zeigerdiagramm erkennen, dass die sich einstellende Phasenverschiebung nicht identisch mit dem Leistungsfaktor der oben angeführten Formeln 3-9 ist.
Nun lassen sich die einzelnen Wirk- und Blindanteile entsprechend aufaddieren und der Scheinwiderstand trigonometrisch lösen. Oder man überführt es zur weiteren Berechnung des Spannungsfalls über die Leitungen in den komplexen Zahlenbereich.

Scheinwiderstand der Leitung

$Z_{L} = R_{L} + j (X_{L, L} - X_{C, L})$

Scheinwiderstand der Verbaucher

$Z_{V} = R_{V} + j (X_{L, V} - X_{C, V})$

Scheinwiderstand gesamt

$Z_{G} = Z_{L} + Z_{V} Z_{G} = R_{L} + R_{V} + j (X_{L, L} + X_{L, V} - X_{C, L} - X_{C, V})$

Spannungsfall über der Leitung

$U_{L} = Z_{L} \cdot I_{B} U_{L} = [R_{L} + j (X_{L, L} - X_{C, L})] \cdot I_{B}$

Da der sich einstellende Strom nicht bekannt ist, muss dieser wie folgt berechnet werden:

$I_{B} = \frac{U_{0}}{Z_{G}}$

Damit resultiert für den Spannungsfall über der Leitung mit einigen Zusammenfassungen:

$U_{L} = U_{0} [\frac{R_{L} + j (X_{L, L} - X_{C, L})}{R_{L} + R_{V} + j (X_{L, L} - X_{C, L} + X_{L, V} - X_{C, V})}] U_{L} = U_{0} [\frac{R_{L} + j X_{L}}{R_{G} + j X_{G}}] U_{L} = U_{0} [\frac{R_{L} R_{G} + X_{L} X_{G}}{{R_{G}}^{2} + {X_{G}}^{2}} + j \frac{X_{L} R_{G} - X_{G} R_{L}}{{R_{G}}^{2} + {X_{G}}^{2}}]$

Die Berechnung sieht schon etwas aufwendiger aus. Hinzu kommt noch, dass man die einzelnen Blindwiderstände erstmal ermitteln bzw. ebenfalls berechnen muss. In der Praxis wird man hier schnell an die Grenzen des Praktikablen stoßen.

[Datum: 16.05.2016]