1. Home
2. Mathematisches
3. Volumen-liegender-Zylinder

Volumen liegender Zylinder

In der Praxis kann es vorkommen, dass man das Volumen bzw. Teilvolumen eines liegenden Zylinders berechnen muss. Dabei kann es sich um einen kreisrunden Behälter handeln, welche teilgefüllt sind. In der praktischen Anwendung können das liegende Silos sein, oder das Behältnis eines Tankwagens oder ein großer Rohrleitungsabschnitt, welcher nur teilgefüllt ist, sein.

In der Praxis lässt sich dann das Volumen meistens nicht direkt messen. Meistens wird dann im liegenden Zylinder nur der Füllstand $h$ gemessen zum Beispiel über eine Druckmessung, Ultraschallmessung, Mikrowellenmessung oder ähnliche Messverfahren. Dass heißt, wenn man das Volumen benötigt, muss man dieses als Funktions über die Höhe $V\left(h\right)$ ausrechnen.

Praktische Anwendungsfälle können sein, dass man eine Volumenregelung in der Automatisierungstechnik realisieren möchte oder eine Nachbestellung bei einem Logistikunternehmen, wenn das Volumen unter einen bestimmten Grenzwert fällt oder eine Abschaltung der Befüllung, wenn das Volumen einen bestimmten Wert erreicht, z.B. bei Mischvorgängen.

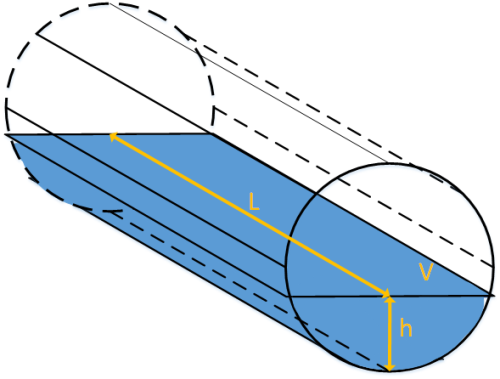
Volumenformel eines liegenden Zylinders

Um es kurz zu machen: Die Formel lautet wie folgt:

$$\begin{gathered} V=L\left(r^{2}arc\cos \left(\frac{r-h}{r}\right)-\left(r-h\right)\sqrt{2rh-h^2}\right) \\ V...Volumen \\ L...Länge des Zylinders \\ r...Radius des Zylinders \\ h...Höhe/Fülls\tan d \end{gathered}$$

Daraus ergibt sich der folgende Kurvenverlauf. Als Länge und Radius des liegenden Zylinders (liegender Behälter) wurde bei diesem Beispiel 1 angenommen.

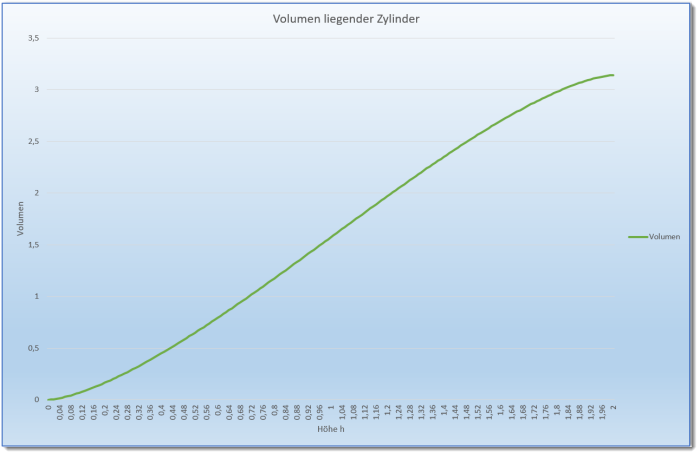
Herleitung Volumenformel eines teilgefüllten liegenden Zylinders

Wie geht man nun an die Herleitung eines solchen Problems heran. Der logische Menschenverstand sagt uns schon mal, dass das Volumen am Anfang, wenn ich einen solchen Behälter beginne zu füllen erstmal langsam anwachsen wird und dann immer schneller. Dort, wo der Behälter am breitesten ist, wird der Anstieg am stärksten sein und zum Ende hin, wenn der Behälter fast voll ist, wird das Volumen wieder langsamer anwachsen. Dies zeigt auch das Diagramm oben. Und mathematisch betrachtet, wäre der Anstieg die erste Ableitung von der Volumenformel.

Überlegen wir weiter: Wenn der Füllstand null ist, dass Volumen auch null sein muss.

$V\left(h=0\right)=0$

Außerdem erscheint es logisch, dass wenn der liegende Zylinder voll ist, es sich um die Volumenformel eines Zylinders handeln muss, welcher sich aus der Länge l des Zylinders multipliziert mit der Kreisfläche zusammensetzt:

$$\begin{gathered} V\left(h=2r\right)=A\times L \\ V\left(h=2r\right)=\mathrm{\pi }\times {\mathrm{r}}^2\times \mathrm{L} \end{gathered}$$

Und ebenfalls logisch erscheint, dass wenn der Behälter nur halb gefüllt ist, dass es dann eben das halbe Zylindervolumen ist.

$$\begin{gathered} V\left(h=2r\right)=\frac{1}{2}A\times l \\ V\left(h=2r\right)=\frac{1}{2}\mathrm{\pi }\times {\mathrm{r}}^2\times \mathrm{L} \end{gathered}$$

Wie kommt man nun aber zu einer Funktion in Abhängigkeit von der Füllstandshöhe h, um auch Zwischenwerte berechnen zu können?

Allgemein berechnet man für das Volumen des liegenden Zylinders die Fläche des Kreissegments As multipliziert mit der Länge L des Zylinders. Da die Länge L konstant ist, beschränkt sich die Herleitung auf die Berechnung der Fläche des Kreissegment.

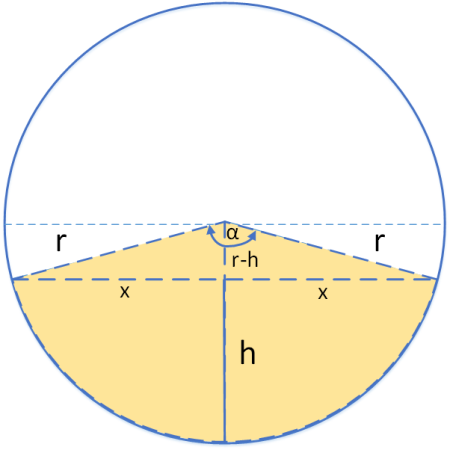
Herleitung Formel Fläche für ein Kreissegment

Bei genauer Betrachtung sieht man, dass man die Kreissegmentfläche As als Subtraktion aus der Kreisbogenfläche AKB und der darüber liegenden Dreiecksfläche AD berechnen kann.

${\mathrm{A}}_{\mathrm{S}}={\mathrm{A}}_{\mathrm{KB}}-{\mathrm{A}}_{\mathrm{D}}$

Berechnung der Kreisbogenfläche

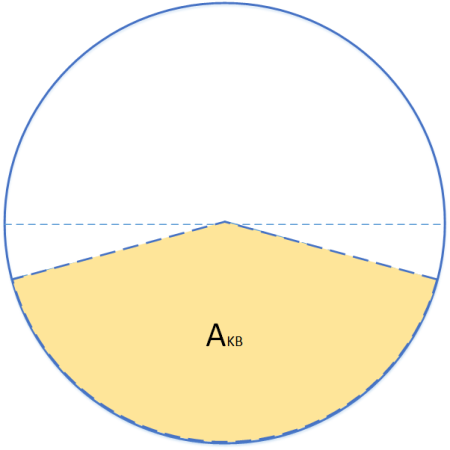
Die Fläche eines Vollkreises berechnet sich bekannter Maßen nach

$\mathrm{A}={\mathrm{\pi r}}^2$

Die Fläches eines Halbkreises ist dann

$\mathrm{A}=\frac{1}{2}{\mathrm{\pi r}}^2$

Man muss also die Flächenformel für den Vollkreis mit dem Winkelverhältnis multiplizieren (Winkel alpha im Bogenmaß)

$$\begin{gathered} {\mathrm{A}}_{\mathrm{KB}}={\mathrm{\pi r}}^2\times \frac{\mathrm{\alpha }}{2\mathrm{\pi }} \\ {\mathrm{A}}_{\mathrm{KB}}=\frac{\mathrm{\alpha }}{2}{\mathrm{r}}^2 \end{gathered}$$

Berechnung der Dreiecksfläche

$$\begin{gathered} {\mathrm{A}}_{\mathrm{D}}=\mathrm{x}(\mathrm{r}-\mathrm{h}) \\ \sin \left(\frac{\mathrm{\alpha }}{2}\right)=\frac{\mathrm{x}}{\mathrm{r}} \\ \mathrm{x}=\mathrm{rsin}\left(\frac{\mathrm{\alpha }}{2}\right) \\ {\mathrm{A}}_{\mathrm{D}}=\mathrm{r}(\mathrm{r}-\mathrm{h})\sin \left(\frac{\mathrm{\alpha }}{2}\right) \\ {\mathrm{A}}_{\mathrm{D}}=({\mathrm{r}}^2-\mathrm{rh})\sin \left(\frac{\mathrm{\alpha }}{2}\right) \end{gathered}$$

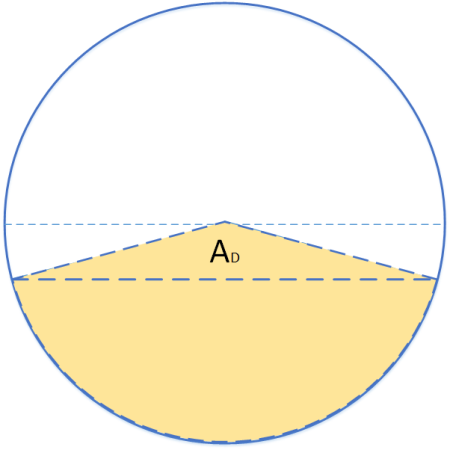
Berechnung des Winkels Alpha

Nun haben wir in unseren Formeln leider noch den Winkle Alpha, der uns leider nicht gegeben ist. Unsere Volumenformel für den liegenden Zylinder soll schließlich nur von Konstanten und der Höhe des Füllstands abhängig sein. Alpha können wir mit folgenden trigenometrischem Zusammenhang berechnen:

$$\begin{gathered} \cos \left(\frac{\alpha }{2}\right)=\frac{r-h}{r} \\ \frac{\alpha }{2}=arc\cos \left(\frac{r-h}{r}\right) \\ \alpha =2arc\cos \left(\frac{r-h}{r}\right) \end{gathered}$$

Für die Kreisbogenfläche folgt daraus:

$A_{KB}=r^{2}arc\cos \left(\frac{r-h}{r}\right)$

Für die Dreiecksfläche ergibt sich:

$A_D=\left(r^2-rh\right)\sin \left(arc\cos \left(\frac{r-h}{r}\right)\right)$

Hierauf wendet man nun folgenden Zusammenhang an:

$\sin \left(arc\cos \left(\beta \right)\right)=\sqrt{1-{\beta }^2}$

Angewendet auf die Dreiecksfläche erhält man:

$$\begin{gathered} A_D=\left(r^2-rh\right)\sqrt{1-{\left(\frac{r-h}{r}\right)}^2} \\ {A}_D=\left(r^2-rh\right)\sqrt{\frac{r^2}{r^2}-\frac{r^2-2rh+h^2}{r^2}} \\ {A}_D=\left(r^2-rh\right)\sqrt{\frac{2rh-h^2}{r^2}} \\ {A}_D=\frac{r^2-rh}{r}\sqrt{2rh-h^2} \\ {A}_D=\left(r-h\right)\sqrt{2rh-h^2} \end{gathered}$$

Subtrahieren wir nun beide Teilflächen voneinander erhalten wir die Kreissegmentfläche:

$A_S=r^{2}arc\cos \left(\frac{r-h}{r}\right)-\left(r-h\right)\sqrt{2rh-h^2}$

Und die mit der Länge des Zylinders multipliziert ergibt die oben bereits angeführte Volumenformel für einen liegenden kreisrunden Behälter in Anhängikeit von seinem Füllstand:

$V=L\left(r^{2}arc\cos \left(\frac{r-h}{r}\right)-\left(r-h\right)\sqrt{2rh-h^2}\right)$

Man kann nun noch die Probe aufs Exemple. Bei einer Füllstandshöhe von null sollte als Ergebnis null herauskommen.

$A_S\left(h=0\right)=0$

Bei einem vollen Behälter, also einer Füllstandshöhe des doppelten Radius, sollte man die Flächenformel für einen Vollkreis herausbekommen.

$A_S\left(h=2r\right)=\mathrm{\pi }{r}^2$

Und für einen Halbkreis die halbierte Fläche eines Vollkreises.

$A_S\left(h=r\right)=\frac{\mathrm{\pi }}{2}{r}^2$

[Datum: 05.03.2018]