Windleistung und Windenergie von Windrädern bzw. Windturbinen berechnen

Überall landein- und landaufwärts sieht man sie: die Windräder oder auch richtiger Weise Windturbinen genannt. Da stellt sich doch die Frage, welche Leistung und welche Energie aus dem Wind idealer Weise gewonnen werden kann? "Idealer Weise" deswegen, weil die nachfolgenden Formeln keine nachgeschalteten Verluste berücksichtigen, die bei der Umwandlung der Windenergie in elektrische Energie entstehen. Verluste entstehen auch konstruktions- und fertigungsbedingt, so dass in der Praxis nie der maximale Wirkungsgrad erreicht werden kann.

Foto einer Windturbine

Formel zur Berechnung der Windleistung an der Windturbine (Windrad)

In Kürze: Die Formel für die Berechnung der maximal möglichen Windleistung an einer Windturbine lautet (Achtung: Es ist die Windleistung und nicht die gewonnene Leistung)

$P = \frac{1}{2} ρ A v^{3} A . . . durchströmte Fläche ρ . . . Dichte der Luft v . . . Windgeschwindigkeit$

Da es sich beim Windrad/Windturbine bei der durchströmten Fläche; den gedachten Strömungskanal; um eine Kreisfläche handelt, kann man auch schreiben:

$P = \frac{1}{2} π ρ r^{2} v^{3} r . . . Radius bzw. Länge Rotorblatt von Mittelpunkt Rotornabe ρ . . . Dichte der Luft v . . . Windgeschwindigkeit$

Zeigt drei Windräder mit der durchströmten Fläche und den Radius des Rotorblatts von der Nabe

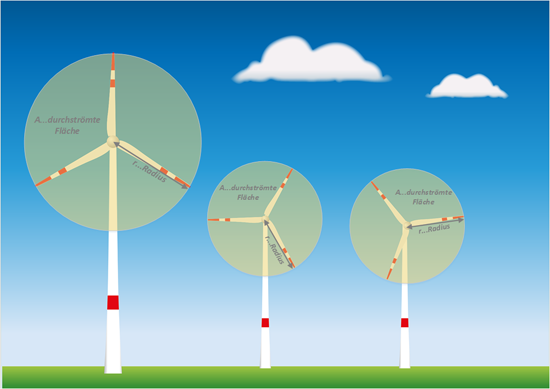
Es sticht gleich ins Auge, dass die Leistung von $v^{3}$ abhängig ist, also vom Kubik der Windgeschwindigkeit. Das bedeutet, dass eine Verdoppelung der Windgeschwindigkeit eine 8-fache Leistung resultiert. Nun stelle man sich mal Wetterlagen oder Gebiete mit großen Windschwankungen vor, was dies im Umkehrschluss für die elektrische Energie und deren Einspeisung ins Netz sowie für die Netzstabilität bedeutet oder Regelalgorithmen, die das ausregeln müssen.

Formel zur Berechnung der Windenergie an der Windturbine (Windrad)

In Kürze: Die Formel für die Berechnung der Windenergie lautet:

$E_{k i n} = \frac{1}{2} m v^{2} m . . . M a s s e v . . . G e s c h w i n d i g k e i t$

Es handelt sich also um die kinetische Energie der bewegten Luftmassen.

Formel Wirkungsgrad bzw. Leistungsbeiwert cp einer Windturbine (Windrad)

In Kürze: Die Formel für die Berechnung der des Leistungsbeiwert cp lautet:

$c_{p} = \frac{P_{N u t z}}{P_{W i n d}}$

Bei einer Windturbine (Windrad) gibt es einen maximalen Leistungsbeiwert, welcher auch Betz'scher Beiwert genannt wird.

$c_{p, m a x} = \frac{16}{27} \approx 0, 5926$

Man kann also theoretisch nur rund 60% der verfügbaren Leistung nutzen. Die realen maximalen Leistungsbeiwerte sind aber aufgrund verschiedener praktischer Verluste bei 0,4 bis 0,5 zu suchen.

Herleitung der Formeln zur Berechnung der Windleistung

Praktische Überlegungen

Nähern wir uns dem Problem mit gesunden Menschenverstand: Betrachtet man Wind, so handelt es sich um bewegte Luftmassen, die durch wetter- oder klimabedingte Druckunterschiede entstehen. Dass sich dies in seiner Ursprungsform auch auf Solarenergie zurückführen lässt, ist ein anderes Thema. Aus der Schulphysik wissen wir, dass bewegte Massen eine bestimmte Energie haben, nämlich die kinetische Energie.

$E_{k i n} = \frac{1}{2} m v^{2} m . . . M a s s e v . . . G e s c h w i n d i g k e i t$

Nun beströmen die bewegten Luftmassen die Windturbine (das Windrad), welches so konstruiert ist, dass es einen Teil der Windenergie in eine Drehbewegung umsetzt, welche nachgelagert im Generator in elektrische Energie umgewandelt wird. Dabei wird dem Wind also Energie entzogen. Da die bewegten Luftmassen konstant bleiben muss sich also die Windgeschwindigkeit nach dem Windrad ändern. Der Wind wird also abgebremst; hat jedoch noch eine verbleibende Restgeschwindigkeit. Daraus können wir schon mal schließen, dass dem Wind nie 100% der Energie entzogen werden können, weil man den Wind dann quasi auf 0 km/h reduzieren würde, wodurch aber die Windströmung zum erliegen kommen würde, die eine Windturbine antreibt. Das macht also keinen Sinn.

Man kann das Ganze auch strömungstechnisch betrachten: Eine Strömung setzt sich immer aus drei Druckanteilen zusammen: dem statischen Druck, dem dynamischen Druck und dem Höhendruck. Da wir uns in einer Ebene bewegen, kann der Höhendruck vernachlässigt werden. Vor der Turbine bzw. direkt an der Windturbine "staut" sich der Wind. Es steigt dort der statische Druck und es sinkt der dynamische Druck (Windgeschwindikeit sinkt).

Passiert der Wind die Turbine, wird die Strömungsgeschwindigkeit weiter sinken und somit würde sich der statische Druck in einem geschlossenen System, wie einer Rohrleitung, weiter erhöhen. Da man hier kein geschlossenes System vorliegen hat, kommt es zum Druckausgleich mit der Umgebung, also einer Ausdehnung des Volumes, was einem Auffächern bzw. Vergrößern des Strömungskanal entspricht.

Darstellung des Strömungskanal einer Windturbine

Andererseits stellen die Rotorblätter einer Windturbine ein Störkörper in der Strömung dar. An diesem kommt es zu Verwirbelungen und inneren Reibungsverlusten, was einen bleibenden Druckverlust erzeugt.

Der Wind wird abgebremst, also wird sich der dynamische Druck hinter der Windturbine verringern und der statische Anteil erhöhen. Es entsteht ein $∆ p$ über der Windturbine.

Mathematische Herleitung der Windleistung

Allgemein ist die Leistung definiert als verrichtete Arbeit innerhalb einer bestimmten Zeit:

$P = \frac{W_{k i n}}{t}$

Setzt man die verrichtete Arbeit, wobei es sich um die bewegten Luftmassen mit einer bestimmten Windgeschwindigkeit handel, ein, so erhält man:

$P = \frac{m v^{2}}{2 t}$

Der Quotient m/t entspricht hier einem Massestrom:

$P = \frac{1}{2} \dot{m} v^{2}$

Zum Massestrom und Volumenstrom lassen sich über die Dicht ineinander umrechen. Und der Volumenstrom ist in unserem Fall eine durchströmte Fläche mit einer bestimmten Geschwindigkeit.

$\dot{m} = ρ \dot{V} = ρ A v$

Ersatzen wir also den Massestrom in unserer Gleichung oben, erhalten wir die Leistungsformel, welche vom Kubik der Windgeschwindigkeit abhängig ist:

$P = \frac{1}{2} ρ A v^{3}$

Herleitung des maximalen Leistungsbeiwertes einer Windturbine

Wie ist nun Herr Betz darauf gekommen, dass die maximal generierbare Leistung einer Windturbine nur (grob aufgerundet) 60% sein kann? Die Herleitung des Betz'schen Leistungsbeiwerts bzw. Betz'schen Gesetzes erstreckt sich über mehrere physikalische und mathematische Zusammenhänge. Dazu betrachtet man die Windturbine als Strömungskanal. Wie so oft in der Physik müssen vereinfachende Annahmen getroffen werden. Wir idealisieren also ein wenig, um es nicht zu kompliziert werden zu lassen:

Über den betrachteten Strömungkanal und Windgeschwindigkeitsbereich nehmen wir an, dass die Dichte der Luft konstant ist, also inkompressibel.
Reibungsverluste werden, wie so oft, vernachlässigt => keine Wärmeverluste

Verwendung der Bernoulli-Gleichung

Für Berechnungen von Strömungen kann man die Bernoulli-Gleichung verwenden. Wie oben schon erläutert betrachten wir nur den statischen und dynamischen Druckanteil. Der Gesamtdruck vor und hinter der Turbine muss demnach gleich sein:

$p_{1} + \frac{ρ v_{1}^{2}}{2} = p_{2} + \frac{ρ v_{2}^{2}}{2} p_{2} - p_{1} = \frac{ρ v_{1}^{2}}{2} - \frac{ρ v_{2}^{2}}{2} ∆ p = \frac{1}{2} ρ (v_{1}^{2} - v_{2}^{2})$

Dies Gleichung benötigen wir später noch einmal.

Verwendung des Impulserhaltungssatzes

Man bedient sich weiterhin des Impulserhaltungssatz und dessen Zusammenhang mit der Kraft. Der Impuls vor und nach dem passieren des Windrads muss gleich sein. (Um eine Verwechslung mit dem Druck zu vermeiden, wird der Impuls hier mit I bezeichnet):

$I_{1} = I_{2} m v_{1} = m v_{2} = k o n s t m (v_{1} - v_{2}) = 0$

Die erste Ableitung des Impulses ist eine Kraft. Dabei handelt es sich um die auf das Windturbinenrad wirkende Kraftkomponente.

$\dot{I} = \frac{d I}{d t} = F$

$F = \frac{m v_{1}}{t} - \frac{m v_{2}}{t} F = \dot{m} v_{1} - \dot{m} v_{2} = \dot{m} (v_{1} - v_{2})$

Bekanntermaßen ist ein Druck eine Kraft auf eine Fläche, wodurch sich folgender formelmäßiger Zusammenhang ergibt:

$∆ p = \frac{F}{A} F = ∆ p A$

Die beiden Kraftgleichungen können wir nun gleichsetzen und ein wenig umstellen:

$\dot{m} (v_{1} - v_{2}) = ∆ p A$

Als nächstes ersetzen wir das $∆ p$ mit der Formel von oben, die wir über den Bernoulli-Zusammenhang hergeleitet haben:

$\dot{m} (v_{1} - v_{2}) = \frac{ρ A}{2} (v_{1}^{2} - v_{2}^{2})$

Nun kann der Massestrom noch mit der Kontinuitätsgleichung ersetzt werden, wobei $v_{0}$ hier die mittlere Windgeschwindigkeit ist, die sich innerhalb der Turbine einstellt :

$ρ A v_{0} (v_{1} - v_{2}) = \frac{ρ A}{2} (v_{1}^{2} - v_{2}^{2}) v_{0} (v_{1} - v_{2}) = \frac{1}{2} (v_{1}^{2} - v_{2}^{2}) v_{0} = \frac{1}{2} \frac{(v_{1}^{2} - v_{2}^{2})}{(v_{1} - v_{2})} = \frac{1}{2} \frac{(v_{1} + v_{2}) (v_{1} - v_{2})}{(v_{1} - v_{2})} v_{0} = \frac{1}{2} (v_{1} + v_{2})$

Berechnung der Nutzleistung über der Windturbine

Um den Betz'schen Leistungsbeiwert zu berechnen, benötigen wir nun noch die Nutzleistung $P_{N u t z}$ , die vom Windrad umgesetzt wird. Die Nutzleistung ist dabei die Differenz aus der Windleistung vor und nach der Windturbine:

$P_{N u t z} = \frac{1}{2} \dot{m} v_{1}^{2} - \frac{1}{2} \dot{m} v_{2}^{2} P_{N u t z} = \frac{1}{2} \dot{m} (v_{1}^{2} - v_{2}^{2})$

Nun ist wieder der Massestrom zu ersetzen:

$P_{N u t z} = \frac{1}{2} ρ A v_{0} (v_{1}^{2} - v_{2}^{2})$

Jetzt noch $v_{0}$ mit der oben dafür hergeleiteten Formel ersetzen:

$P_{N u t z} = \frac{1}{4} ρ A (v_{1} + v_{2}) (v_{1}^{2} - v_{2}^{2})$

Aus taktischen Gründen werden jetzt die Klammerausdrücke ausmultipliziert und dann $v_{1}^{3}$ ausgeklammert:

$P_{N u t z} = \frac{1}{4} ρ A (v_{1}^{3} - v_{1} v_{2}^{2} + v_{1}^{2} v_{2} - v_{2}^{3}) P_{N u t z} = \frac{1}{4} ρ A v_{1}^{3} (1 - \frac{v_{2}^{2}}{v_{1}^{2}} + \frac{v_{2}}{v_{1}} - \frac{v_{2}^{3}}{v_{1}^{3}})$

Aus dem Klammerausdruck lässt sich jetzt mit mathematischer Trickserei zwei Klammerausdrücke machen:

$P_{N u t z} = \frac{1}{4} ρ A v_{1}^{3} (1 + \frac{v_{2}}{v_{1}}) (1 - \frac{v_{2}^{2}}{v_{1}^{2}})$

Berechnung des Leistungsbeiwertes

Nun setzt man die Formeln für die durch die Windturbine gewonnene Nutzleistung ins Verhältnis zur Windleistung

$C_{P} = \frac{P_{N u t z}}{P_{W i n d}} C_{P} = \frac{2 ρ A v_{1}^{3}}{4 ρ A v_{1}^{3}} (1 + \frac{v_{2}}{v_{1}}) (1 - \frac{v_{2}^{2}}{v_{1}^{2}}) C_{P} = \frac{1}{2} (1 + \frac{v_{2}}{v_{1}}) (1 - \frac{v_{2}^{2}}{v_{1}^{2}})$

Für die weitere Berechnung wird weiter getrickst und man setzt

$x = \frac{v_{2}}{v_{1}}$

Wodurch sich die Leistungsbeiwert-Gleichung vereinfachen lässt zu:

$C_{P} = \frac{1}{2} (1 + x) (1 - x^{2})$

Berechnung des maximalen Leistungsbeiwertes

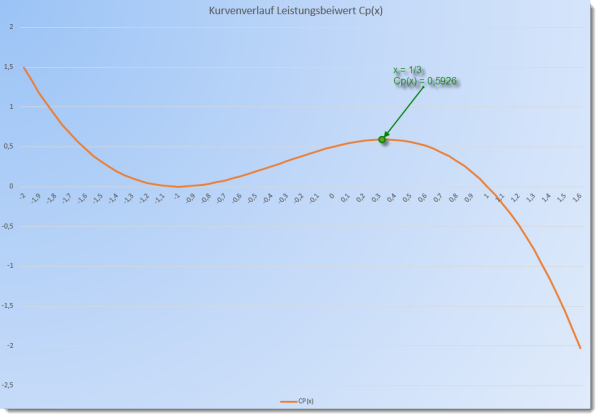
Um den maximalen Leistungsbeiwert nach Betz zu berechnen, können wir berechnen an welcher Stelle X maximal wird. Dazu multiplizieren wir die Formel aus und bilden die erste Ableitung:

$C_{P} = \frac{1}{2} (1 - x^{2} + x - x^{3}) = - \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + \frac{1}{2} x + \frac{1}{2} C_{P}^{'} = - \frac{3}{2} x^{2} - x + \frac{1}{2}$

Zur Berechnung des Maximums wird die Gleichung null gesetzt und über die quadratische Lösungsformel x bestimmt.

$0 = - \frac{3}{2} x^{2} - x + \frac{1}{2} 0 = x^{2} + \frac{2}{3} x - \frac{1}{3} x_{1, 2} = - \frac{1}{3} \pm \sqrt{\frac{1}{9} + \frac{3}{9}} = - \frac{1}{3} \pm \frac{2}{3} x_{1} = - 1 x_{2} = \frac{1}{3}$

Die erste Lösung ist negativ und die zweite Lösung ist positiv. Schauen wir noch kurz über die zweite Ableitung wo sich Minimum und Maximum befinden:

$C_{P}^{''} (x) = - 3 x - 1 C_{P}^{''} (- 1) = 2 (2 > 0 ... Minimum) C_{P}^{''} (\frac{1}{3}) = - 2 (-2 < 0 ... Maximum)$

Nun können wir den maximalen Leistungsbeiwert ermitteln. Das Ergebnis von $x_{2}$ wird in die Gleichung des Leistungsbeiwert $C_{P} (x)$ wieder eingesetzt.

$C_{P} = \frac{1}{2} (1 + \frac{1}{3}) (1 - \frac{1}{9}) = \frac{1}{2} \times \frac{4}{3} \times \frac{8}{9} C_{P} = \frac{16}{27} \approx 0, 5926$

Darstellung des Kurvenverlaufs des Leistungsbeiwertes in Abhängigkeit vom Verhältnis der Windgeschwindigkeit vor und nach der Windturbine

[Datum: 11.03.2018]